Квантовая теория поля в физике высоких энергий
научный сотрудник, к.ф.-м.н. Н. П. Мещеряков
Методы квантовой теории поля (КТП) используются во многих областях современной физики: в физике фундаментальных взаимодействий, атомной и ядерной физике, космологии, физике конденсированного состояния вещества. Этот список можно продолжать, но даже из такого неполного перечня очевидно, что изучение КТП является основой для глубокого понимания законов природы.
Обобщая квантовую механику на случай систем с бесконечным числом степеней свободы, удовлетворяющих требованию релятивистской инвариантности, КТП позволяет описывать процессы, в которых число частиц может изменяться. С практической точки зрения, методы КТП применяются в физике частиц для вычисления различных наблюдаемых величин, которые можно сравнивать с экспериментальными данными, например, сечения рассеяния или ширины распада. Для этого используется теория возмущений по малому параметру – константе связи, и, как следствие, результат будет представляться в виде степенного ряда. При этом вычисления могут быть упорядочены и графически представлены в виде т.н. диаграмм Фейнмана. Например, ведущим членам ряда соответствуют древесные диаграммы без петель.
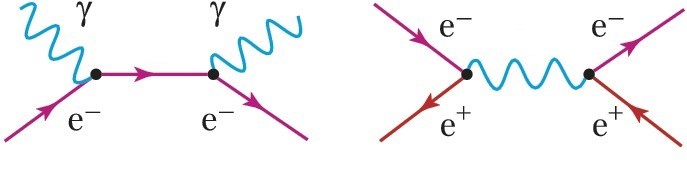
Рисунок 1: примеры древесных диаграмм Фейнмана в квантовой электродинамике, дающих вклад в комптоновское рассеяние (слева) и аннигиляцию и рождение электрон-позитронной пары (справа)
Спецкурс кафедры «Основы квантовой теории поля» посвящен подробному введению в формализм КТП и включает, как каноническое квантование свободных теорий скалярного, спинорного и электромагнитного поля, так и квантование теорий поля со взаимодействием в рамках теории возмущений, в том числе обоснование диаграммной техники Фейнмана. Решение задач по КТП рассматривается на спецкурсе «Дополнительные главы квантовой теории поля». Одним из результатов освоения данных дисциплин станет умение применять метод диаграмм Фейнмана, в частности, для вычисления сечений рассеяния в квантовой электродинамике в ведущем порядке.
Рассмотрение следующих порядков теории возмущений приводит к необходимости вычислять фейнмановские диаграммы с петлями – т.н. радиационные поправки. В этом случае возникает проблема, которая представляется, на первый взгляд, фатальной: радиационные поправки даются интегралами по петлевым импульсам и эти интегралы расходятся! Однако для определенного класса теорий последовательное решение этой проблемы во всех порядках теории возмущений было найдено. Оно основано на использовании методов регуляризации и перенормировки. Сперва расходящиеся интегралы регуляризуют, т.е. делают их конечными, и проводят вычисления в регуляризованной теории. Затем расходимости устраняют, переопределяя (перенормируя) параметры и поля, входящие в исходный лагранжиан теории. В результате, итоговое выражение для радиационных поправок будет конечным в пределе снятия регуляризации. Таким образом, владение методами теории перенормировок совершенно необходимо для сравнения теоретических результатов с экспериментальными данными.
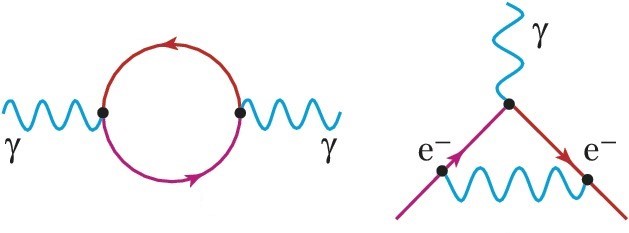
Рисунок 2: примеры однопетлевых диаграмм Фейнмана в квантовой электродинамике, дающих вклад в поляризацию вакуума (слева) и аномальный магнитный момент электрона (справа)
Методы вычисления радиационных поправок, способы регуляризации расходимостей и основы процедуры перенормировок излагаются в спецкурсе «Перенормировки в квантовой теории поля». Различные приложения теории перенормировок и дополнительные аспекты формализма, в частности, метод ренормализационной группы, разбираются на конкретных примерах и задачах в спецкурсе «Ренормгруппа в квантовой теории поля».
Одним из главных достижений, связанным с развитием методов КТП, стало построение Стандартной модели сильных и электрослабых взаимодействий. Стандартная модель является чрезвычайно успешной теорией: полученные на ее основе теоретические предсказания с высокой точностью согласуются почти со всеми данными, которые предоставлены экспериментами на ускорителях частиц. Тем не менее, имеется ряд явлений, которые не удается объяснить, не прибегая к ее модификации (даже оставляя в стороне проблему квантования гравитации), например: нейтринные осцилляции, барионная асимметрия, темная материя. Кроме того, некоторые теоретические аспекты устройства Стандартной модели также свидетельствуют о том, что ее следует рассматривать как низкоэнергетический предел более фундаментальной теории. Известно много вариантов расширения Стандартной модели. Пожалуй, наиболее элегантный из них основан на использовании одной интересной концепции – суперсимметрии, связывающей фермионные и бозонные степени свободы. Например, суперсимметричные обобщения Стандартной модели предоставляют вероятных кандидатов на роль частиц темной материи; решают проблему тонкой подстройки массы бозона Хиггса, благодаря сокращению квадратично расходящихся радиационных поправок; допускают объединение взаимодействий на некотором очень высоком энергетическом масштабе, тем самым указывая направление дальнейшего обобщения – построение суперсимметричных теорий Великого объединения.

Рисунок 3: поведение бегущих констант связи , и , соответствующих калибровочным группам U(1), SU(2), SU(3), при изменении масштаба энергий в Стандартной модели (слева) и Минимальной суперсимметричной стандартной модели (справа)
Прямой поиск суперсимметричных частиц (суперпартнеров частиц Стандартной модели) ведется на самом крупном современном ускорителе частиц – Большом адронном коллайдере. Продолжаются и активные теоретические исследования суперсимметричных теорий. Большой интерес вызывает изучение замечательных квантовых свойств суперсимметричных калибровочных теорий, которые обусловлены нетривиальной взаимосвязью между расходимостями в таких теориях. Данной тематикой занимается н.с., к.ф.-м.н. Н.П. Мещеряков.
Таким образом, успешное освоение спецкурсов кафедры, посвященных изложению методов КТП, откроет дальнейшие перспективы для научной работы в различных передовых областях физики высоких энергий и смежных направлениях, использующих аналогичный математический аппарат.
Основы квантовой теории поля [7 семестр]
Квантовая теория поля является теоретической основой физики высоких энергий и физики элементарных частиц. Вместе с тем, методы квантовой теории поля нашли широкое применение и в других областях современной физики, например, в статистической физике и физике конденсированного состояния вещества, гравитации и космологии. В физике частиц методы квантовой теории поля применяются, например, для вычисления различных наблюдаемых величин (таких как сечения процессов рассеяния или ширины распада), которые можно сравнивать с экспериментальными данными. В данном курсе даются базовые знания в области квантовой теории поля.
1. Квантовая теория поля и физика фундаментальных взаимодействий. Этапы развития КТП. Обзор математического аппарата КТП.
2. Квантовая теория систем тождественных частиц. Принцип неразличимости. Бозоны и фермионы. Операторы рождения и уничтожения. Канонические перстановочные соотношения.
3. Пространство Фока. Операторы наблюдаемых величин. Квантовые поля.
4. Алгебры Грассмана.
5. Требования релятивистской инвариантности в КТП. Симметрии и законы сохранения. Теорема Нетер.
6. Свободное скалярное поле. Интегралы движения. Перестановочные функции.
7. Свободное спинорное поле.
8. Массивное векторное поле. Условие Лоренца и физические степени свободы.
9. Безмассовое векторное поле. Индефинитная метрика.
10. Постановка задачи рассеяния в КТП. Матрицы рассеяния.
11. Хронологическое произведение операторов. Теорема Вика.
12. Построение S-матрицы в теории возмущений.
13. Фейнмановская диаграммная техника. Алгоритмы вычисления наблюдаемых величин в теории возмущений.
14. Производящий функционал функций Грина. Редукционные формулы.
15. Функциональные интегралы в КТП.
16. Производящий функционал связных функций Грина.
17. Основы теории калибровочных полей. Принцип локальной калибровочной инвариантности. Квантовая электродинамика.
18. Неабелевы калибровочные поля. Теория Янга-Миллса.
19. Спонтанное нарущение симметрии в калибробровочных теориях. Механизм Хиггса. Унитарная калибровка и спектр масс физических частиц.
20. Стандартная модель фундаментальных взаимодействий. Требование симметрии и структура лагранжиана.
Литература:
1. М. Пескин, Д. Шредер. Введение в квантовую теорию поля. Москва-Ижевск: РХД, 2001.
2. Н.Н. Боголюбов, Д.В. Ширков. Введение в теорию квантованных полей. Москва: Наука, 1984.
3. Н.Н. Боголюбов, Д.В. Ширков. Квантовые поля. Москва: Физматлит, 2005.
4. К. Ициксон, Ж.Б. Зюбер. Квантовая теория поля. ТТ 1 и 2. Москва: Мир, 1984.
5. М.Н. Дубинин, В.А. Ильин, Д.А. Славнов. Основы квантовой теории поля, часть 1, Издательство Московского Университета, 1984.
6. М.Н. Дубинин, В.А. Ильин, А.Е. Пухов, Д.А. Славнов. Основы квантовой теории поля, часть 2, Издательство Московского Университета, 1985.
7. В.А. Ильин, А.Е. Пухов, Д.А. Славнов. Основы квантовой теории поля, часть 3, Издательство Московского Университета, 1988.
8. А.А. Славнов. Лоренц-инвариантная квантовая теория Янга-Миллса без неоднозначностей Грибова. ТМФ. Т. 154, с. 204-211, 2009.
9. Б.Л. Воронов, Д.М. Гитман, И.В. Тютин. Гамильтониан Дирака со сверхсильным кулоновским полем. ТМФ. Т. 150, с. 41-48, 2007.
10. Д.В. Ширков, И.Л. Скворцов. Десятилетие аналитической теории возмущений. ТМФ. Т.150, с 152-176, 2007.
Перенормировки и ренормгруппа в квантовой теории поля [8-й семестр]
Теория перенормировок является одним из важнейших разделов квантовой теории поля. Именно процедура перенормировок делает содержательным метод теории возмущений, применительно к квантовой теории поля. Дело в том, что радиационные поправки, которые представляются диаграммами Фейнмана, содержащими петли, как правило, даются расходящимися интегралами. Решение этой проблемы основано на использовании методов регуляризации и перенормировки. Таким образом, владение данными методами совершенно необходимо для сравнения теоретических результатов с экспериментальными данными.
1. Перестановочные функции квантовой теории поля как обобщенные функции.
2. Ультрафиолетовые расходимости и их регуляризация.
3. Регуляризация Паули-Виларса.
4. Размерная регуляризация.
5. Общие сведения о процедуре перенормировок.
6. Примеры расходящихся диаграмм Фейнмана, индекс расходимости.
7. R-операция.
8. Константы перенормировки.
9. Перенормировка и симметрия, тождества Уорда.
10. Тождества Уорда в электродинамике.
11. Ренормгруппа.
12. Уравнения ренормгруппы.
13. Ренормгруппа в электродинамике.
14. Ренормгруппа в неабелевых калибровочных моделях.
15. Асимптотическая свобода.
Литература:
1. М. Пескин, Д. Шредер. Введение в квантовую теорию поля. Москва-Ижевск: РХД, 2001.
2. Н.Н. Боголюбов, Д.В. Ширков. Введение в теорию квантованных полей. Москва: Наука, 1984.
3. Н.Н. Боголюбов, Д.В. Ширков. Квантовые поля. Москва: Физматлит, 2005.
4. Дж. Коллинз. Перенормировка. Москва: Мир, 1988.
5. В.А. Ильин, А.Е. Пухов, Д.А. Славнов. Основы квантовой теории поля, часть 3, Издательство Московского Университета, 1988.
6. Р.Н. Баранов. Однопетлевые контрчлены в теории Янга-Миллса с калибровочно-инвариантным духовым лагранжианом. ТМФ. Т. 161, с. 37-45, 2009.
7. А.А. Славнов. Локальная калибровочно-инвариантная инфракрасная регуляризация теории Янга-Миллса. ТМФ. Т. 154, с. 210-219, 2008.
8. А.Б. Пименов, К.В. Степаньянц. Двухпетлевая функция Гелл-Мана-Лоу. ТМФ. Т. 155, с. 398-414, 2008.
Схемы перенормировки в квантовой теории поля [11 семестр]
В круг актуальных задач квантовой теории поля, безусловно, входит вычисление квантовых поправок в достаточно высоких порядках теории возмущений. Для решения задач такого рода совершенно необходимо владеть методами регуляризации и перенормировки. Курс предоставляет детальное обсуждение основных видов регуляризации и схем вычитания, используемых в современной квантовой теории поля. На конкретных примерах демонстрируются особенности применения различных техник перенормировки, обсуждаются их преимущества и недостатки. Большое внимание уделяется общему анализу структуры рядов теории возмущений, исследованию схемной зависимости и калибровочной зависимости квантовых поправок.
1. Обзор основных видов регуляризации: обрезание по импульсу, регуляризация Паули—Вилларса, регуляризация высшими ковариантными производными, размерная регуляризация, размерная редукция, аналитическая регуляризация.
2. Схема перенормировки Боголюбова—Парасюка—Хеппа—Циммермана. R-операция и лесная формула. Отсутствие необходимости регуляризации.
3. Зависящие и не зависящие от массы схемы вычитаний. Отличие в ренормгрупповых уравнениях. Схема вычитаний на массовой поверхности. Схема импульсных вычитаний.
4. Минимальные вычитания и модифицированные минимальные вычитания в размерной регуляризации и размерной редукции. Связь между двумя размерными техниками. Проблема .
5. Регуляризация высшими ковариантными производными. Преимущества и недостатки по сравнению с размерной техникой.
6. Связь физических параметров с перенормированными. Не зависящие от выбора схемы перенормировки физические свойства уравнений ренормгруппы (существование фиксированных точек, наклон -функции в нуле, значение аномальной размерности в нуле).
7. Калибровочная зависимость/независимость ренормгрупповых функций и калибровочная независимость физических предсказаний ренормгрупповых уравнений.
8. Перенормировка теорий с глобальными и калибровочными симметриями в отсутствие инвариантной регуляризации. Алгебраическая перенормировка. Универсальная калибровочно-инвариантная перенормировка.
9. Методы оптимизации рядов теории возмущений для наблюдаемых величин. Понятие эффективного заряда. Соразмерные масштабы. Принцип скорейшей видимой сходимости. Принцип минимальной чувствительности. Процедура Бродского—Лепажа—Маккензи. Принцип максимальной конформности.
Основная литература:
1. Пескин М., Шрёдер Д. Введение в квантовую теорию поля. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 784 с.
2. Боголюбов Н.Н., Ширков Д.В. Введение в теорию квантованных полей. – М.: URSS: ЛЕНАНД, 2018. – 643 с.
3. Славнов А.А., Фаддеев Л.Д. Введение в квантовую теорию калибровочных полей. – М.: URSS: ЛЕНАНД, 2017. – 272 с.
4. Коллинз, Джон. Перенормировка. Введение в теорию перенормировок, ренормализационной группы и операторных разложений. – М.: Мир, 1988. – 446 с.
5. Иоффе Б.Л., Липатов Л.Н., Фадин В.С. Квантовая хромодинамика: пертурбативные и непертурбативные аспекты. Кн. 1. – М.: ЦСПиМ, 2012. – 412 c.
6. Иоффе Б.Л., Липатов Л.Н., Фадин В.С. Квантовая хромодинамика: пертурбативные и непертурбативные аспекты. Кн. 2. – М.: ЦСПиМ, 2013. – 346 c.
7. Славнов А.А. Не зависящая от регуляризации калибровочно-инвариантная перенормировка теории Янга—Миллса // Теоретическая и математическая физика. – 2002. – Т. 130. – С. 3—14.
8. Dominik Stöckinger. Regularization by Dimensional Reduction: Consistency, Quantum Action Principle, and Supersymmetry // Journal of High Energy Physics. – 2005. – Vol. 2005, no. 3. – P. 076 [arXiv: 0503129 [hep-ph]].
9. Piguet, Oliver., Sorella, Silvio P. Algebraic renormalization. Perturbative renormalization, symmetries and anomalies. – Berlin (etc.): Springer, 1995, 134 p.
10. Alexandre Deur, Stanley J.Brodsky, Guy F.de Téramond. The QCD Running Coupling // Progress in Particle and Nuclear Physics. – 2016. – Vol. 90. – P. 1–74 [arXiv: 1604.08082 [hep-ph]].
11. Stanley J. Brodsky, Hung Jung Lu. Commensurate Scale Relations in Quantum Chromodynamics // Physical Review D. – 1995. – Vol. 51. – P. 3652-3668 [arXiv: 9405218 [hep-ph]].
12. Stanley J. Brodsky, Leonardo Di Giustino. Setting the Renormalization Scale in QCD: The Principle of Maximum Conformality // Physical Review D. – 2012. – Vol. 86. – P. 085026-1—085026-11 [arXiv: 1107.0338 [hep-ph]].
13. G. Grunberg. Renormalization Scheme Independent QCD and QED: The Method of Effective Charges // Physical Review D. – 1984. – Vol. 29. – P. 2315—2338.
14. P.M. Stevenson. Optimized Perturbation Theory // Physical Review D. – 1981. – Vol. 23. – P. 2916—2944.
Дополнительная литература:
1. Methods in Field Theory / R. Balian, J. Zinn-Justin. (Eds.) – Singapore (etc.): World Scientific; Amsterdam (etc.): North-Holland, 1993. – 408 p.
2. Andrey Grozin. Lectures on QED and QCD // ArXiv e-prints. — 2005. — no. 0508242 [hep-ph].








