АНАТОЛИЙ АЛЕКСАНДРОВИЧ ВЛАСОВ

К столетию со дня рождения
  К 75-летию физфака
    К семидесятилетию уравнений Власова

     В этом 2008 году, 20 августа, исполнилось сто лет со дня рождения Анатолия Александровича Власова – выдающегося физика-теоретика ХХ столетия, вошедшего именем в историю физики. Термины «кинетические уравнения Власова», «уравнения Власова-Максвелла» сегодня можно встретить не только в текстах научных статей авторитетных физических журналов, но и в наименованиях отдельных глав в учебниках и монографиях. Развитый А.А.Власовым метод с успехом используется в исследованиях по физике плазмы, физике металлов, ядерной физике, физике атмосферы, астрофизике, физической химии и т.п.
     Фундаментальное исследование А.А.Власова «О вибрационных свойствах электронного газа» было опубликовано в «Журнале экспериментальной и теоретической физике» в 1938 году , 70 лет тому назад.
     В 1967 году эта работа была признана в числе наиболее выдающихся достижений советской  физики и снова опубликована в «Успехах физических наук».
    Достаточно подробная  биография А.А.Власова и его «мировая линия» на физическом факультете МГУ, где он работал профессором, а с1945 по 1953 год – заведующим кафедрой теоретической физики, помещена на сайте его родного города Балашова Саратовской области, на других сайтах, в энциклопедиях и энциклопедических справочниках, а также в книге «Анатолий Александрович Власов» из серии «Выдающиеся ученые физического факультета МГУ».
    Статья А.А.Власова «О вибрационных свойствах электронного газа» появилась в свет, когда под физической кинетикой  понималась наука, центральным уравнением которой было кинетическое уравнение Больцмана подобно тому, как центральными уравнениями электродинамики служат уравнения Максвелла.
    Уравнение Больцмана в простейшем случае, для частиц без внутренних степеней свободы, обычно представляется в виде (см. «Физическую энциклопедию»)
Здесь f – функция распределения, t,x,p – независимые переменные,  слагаемое с  сохраняем несмотря на то, что и в уравнении  нет функции для которой определено понятие полной производной по времени.
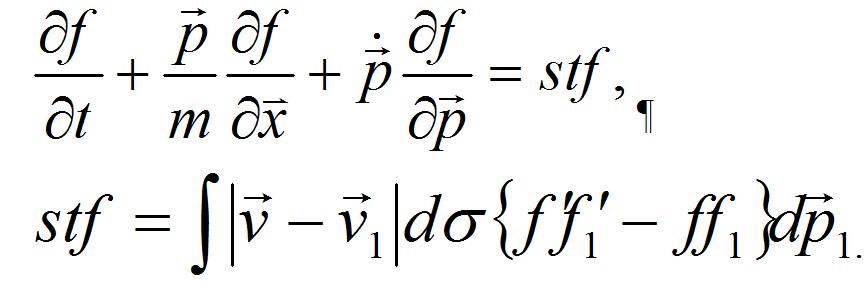
     А.А. Власов предложил систему уравнений, принципиально отличающихся от уравнения Больцмана. Для простейшего случая эволюции электронной компоненты в условиях, когда ионную компоненту можно считать неподвижной, эта система имеет вид:
     Исторический опыт развития физики свидетельствует, что новые знания, как правило, являются достоянием  последующих поколений, а первопроходцы-одиночки подвергаются жестокой критике. Например, реакция  В.Гайзенберга на появление уравнения Э.Шредингера была следующей: «чем больше я размышляю о физической стороне теории Шредингера, тем ужаснее она мне кажется».
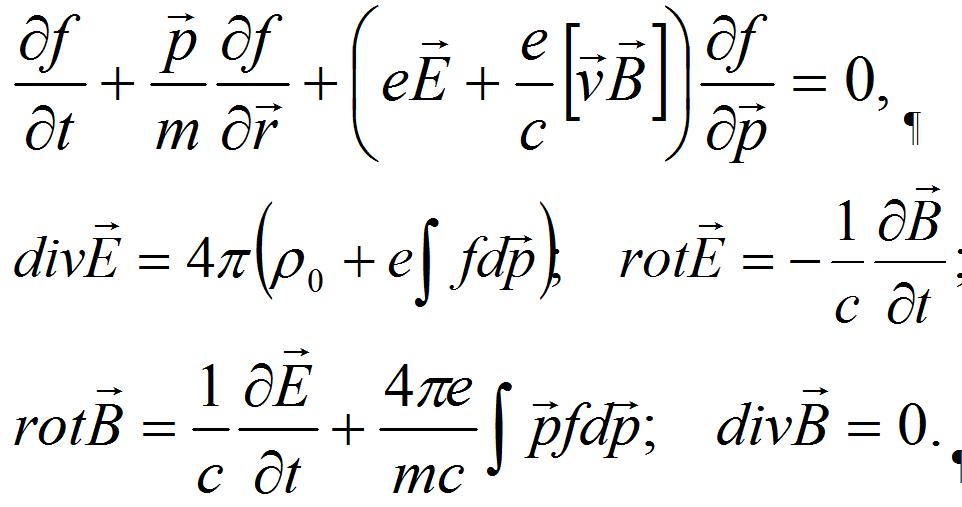
     У А.А. Власова, как и у Э.Шредингера, также были предшественники. Годом раньше, в 1937 году, в том же журнале ЖЭТФ Л.Д.Ландау опубликовал работу, в которой уравнение Больцмана было модифицировано для случая кулоновских взаимодействий. Фактически в уравнении Больцмана в качестве дифференциального сечения рассеяния d? была использована формула Резерфорда, соответствующая рассеянию на малые углы. Интеграл столкновений при этом оказался расходящимся и автору пришлось прибегнуть к его искусственному обрезанию. Статья Ландау породила самостоятельное направление в физике, связанное с дальнейшим совершенствованием интеграла столкновений Ландау на случай учета влияния на парные столкновения частиц их взаимодействия с волнами, которые могут возбуждаться в плазме. Это направление представлено работами В.П.Силина, Ю.Л.Климонтовича, Р.Балеску, А.Ленарда, Р.Л.Гернси и др.
     В уравнении Власова интеграла столкновений нет вообще (на основе оценок собственных частот системы и частот столкновений А.А.Власов приходит к выводу, что интегралами столкновений можно пренебречь). Поэтому  кажется, что А.А.Власов «забыл» интеграл столкновений и его следует восстановить, а  в уравнении Больцмана «не учтёна» сила Лоренца, и её тоже следует восстановить (!) прежде чем проводить конкретные исследования. Уравнения, полученные путем такого примирения идей, иногда кладутся в основу исследований и в наши дни.
     Такой подход не имеет под собой оснований. Дело в том, что любое классическое уравнение, в котором дискретный набор частиц микромира представляется гладкими функциями, существует только на определённых пространственно-временных масштабах. В уравнении Больцмана детальная картина взаимодействий в терминах сил и потенциалов и движения, как непрерывной смены состояний, заменена на картину рассеяния, основанную на анализе только двух состояний, «до» и «после» рассеяния, разнесенных на конечное время. Учет бесконечно близких состояний привел бы к появлению производной функции распределения по импульсам вместо конечной разности произведений функций распределения в уравнении Больцмана.
     Замена детальной картины взаимодействий, на картину столкновений возможна при условии, что частицы движутся достаточно долго (длина свободного пробега велика) как однородный по сечению монохроматический пучок без какого-либо взаимодействия, а само взаимодействие представляется кратковременным актом и происходит на малых расстояниях. Иными словами, радиус взаимодействия ? частиц должен быть намного меньшим длины свободного пробега ?.  Следовательно. характерный масштаб l, на котором может иметь место уравнение Больцмана в приведенном выше виде, должен превышать радиус взаимодействия ?. (На таком масштабе исчезает детальная картина взаимодействий, потенциалы взаимодействий и детали траекторий; остается лишь результат – отклонение на определённый угол рассеяния.) C другой стороны характерный масштаб l, очевидно, должен быть много меньшим длины свободного пробега. Таким образом, ? « l « ?. Аналогичное требование накладывается и на минимальный временной интервал t, который должен превышать  характерное время взаимодействия двух частиц, но быть малым по сравнению со средним временем свободного пробега.
     Будем теперь искусственно увеличивать радиус действия сил ?., полагая неизменными остальные параметры системы частиц. Как только радиус взаимодействия начнёт превышать ?, указанное неравенство становится противоположным, длина свободного пробега стремится к нулю и условия существования уравнения Больцмана перестают выполняться. Так как полное сечение рассеяния пучков частиц с кулоновским взаимодействием расходится, радиус взаимодействия равен бесконечности, и уравнение Больцмана исчезает значительно раньше, чем мы перейдем к закону Кулона. Поэтому подставлять в уравнение Больцмана формулу Резерфорда или её приближенное выражение, соответствующее рассеянию на малые углы, не имеет смысла.
     Из этого простого анализа  видно также, каким должно быть кинетическое уравнение в пределе бесконечного  большого радиуса взаимодействия. В этом пределе каждая частица-источник силового поля, в том числе и поля излучения, все время движется  в поле других частиц, и это движение не сводится к простой последовательности парных столкновений. В сферу действия каждой заряженной частицы попадают, вообще говоря, все частицы системы. «Плазма – это не газ, а своеобразная система, стянутая далекими силами»,- замечает А.А.Власов. В уравнениях Власова состояние системы частиц из определенной окрестности пространственной точки с определенными значениями импульса, представленное функцией распределения, изменяется со временем в электромагнитном поле, созданном в соответствии с законами электродинамики всем коллективом частиц. Пространственные масштабы, на которых имеет место уравнение Власова с самосогласованным полем, те же, что и в электродинамике сплошных сред. Плотность заряда и электрического тока определены на физически бесконечно малых объемах, которыми также представлена указанная выше пространственная окрестность определения функции распределения. Электромагнитные поля в  уравнениях Власова  определяют взаимодействия именно таких коллективов частиц, а не отдельных электронов. Несмотря на то, что этот очевидный факт следует  уже из уравнения divЕ =4?? для гладких ? (Е – это не то поле, которое действует на отдельный заряд), он нередко является источником ошибок.  Ни сами фундаментальные идеи Власова, положенные в основу создания теории коллективных явлений в системах частиц с электромагнитным взаимодействием, ни их количественное оформление не связаны с представлениями об ансамблях Гиббса и средних по ансамблю. Власов А.А. неоднократно и в различных формулировках подчеркивал, что «представления об ансамблях Гиббса противоречат духу электродинамики». Но это может означать только то, что уравнения Власова и гиббсова статистическая физика – разные науки, построенные на разных, не совпадающих между собой  определениях вероятностей. Следует заметить также, что гамильтониан системы заряженных частиц и уравнение Лиувилля в их обычном понимании существуют только с точностью до v2/c2, недопустимой при построении теории, в которой скорости частиц v могут принимать произвольные, возможно меньшие скорости света с, значения. К сожалению, эту идею, к реализации которой был подключен автор этих строк, при жизни Власова не удалось довести до состояния рабочего  метода.
      Здесь мы не имеем возможности более глубоко обсуждать эти идеи, однако упоминание о них необходимо, так как ими представлены минимальные сведения, необходимые для понимания сути многих  высказываний Власова, и, в частности, - о механике: «механика – это не наука» и подобных – о теории поля. Власов ясно понимал, что это только две «асимптотические» ветви единой, реализованной в природе науки, в которой частицы движутся в полях,  которые они создают сами (а не только в заданном внешнем поле) и которые управляют их движением посредством полей, источники которых (плотности заряда и электрического тока) не являются  заданными функциями. Уравнения Власова являются частной реализацией этой общей схемы с замкнутой нелинейностью для коллективных процессов на уровне средних физической кинетики.
     Однако А.А.Власов в своей работе пошел дальше. Он разработал новый метод решения своих нелинейных  интегро-дифференциальных уравнений. Этот метод в современной интерпретации иногда называется методом разложения по амплитудам поля. В цитируемой работе  А.А.Власова использовано только линейное приближение, и на этой основе введено понятие о дисперсионных уравнениях, найдены дисперсионные формулы для продольных и поперечных волн в плазме с максвелловским распределением по скоростям, а также для электронного газа с распределением Ферми в металлах. Однако Власов указывает, что только в линейной теории «наличие продольных волн не связано с поперечными, и наоборот. Вследствие того, что исходные уравнения нелинейны, уже в следующем приближении должно выступить их взаимодействие. Наличие одних должно вызвать другие». И далее: «Решение этой задачи должно заключаться в дальнейшем приближении исходной нелинейной системы (II).  Это замечание относится также и к оптике металлов (главным образом щелочных) в ультрафиолете, где выступает инерция электронов и где теория строится по тому же типу, как и для ионосферы».
      Среди первых дальнейших успешных методов анализа уравнений Власова следует отметить разработанную в трудах  А.А.Веденова, Е.П.Велихова, Р.З.Сагдеева  квазилинейную теорию, позволяющую учитывать влияние колебаний на неосциллирующую часть функции распределения частиц. В разработку современных методов нелинейных явлений в плазме, учитывающих квадратичную, кубическую и т.д. нелинейность, описывающих нелинейное взаимодействие волн с различными поляризациями, взаимодействие волн захваченными частицами, динамику солитонов и т.п. внесли существенный вклад  А.А.Ахиезер, В.Н.Цытович, В.П.Силин, А.Г.Ситенко, Б.Б.Кадомцев, А.А.Рухадзе, В.Н.Ораевский, В.Л.Якименко, Р.В.Хохлов и многие другие отечественные и зарубежные ученые.
     Однако прежде работа А.А.Власова была подвергнута жесточайшей критике. В научных статьях  появились заголовки объявлявшие несостоятельными представлений Власова, ошибочными уравнения Власова и т.п. Критическая статья "О несостоятельности работ А. А. Власова по обобщённой теории плазмы и теории твёрдого тела", (ЖЭТФ,1946) выходит за подписью В.А.Фока, М.А. Леонтовича, Л.Д.Ландау В.Л.Гинзбурга. В публикации ответной статьи А.А.Власову отказано. Одновременно в том же году Л.Д.Ландау публикует новое решение «несостоятельных» уравнений Власова, в котором  интеграл в смысле главного значения в расчетах Власова продольной диэлектрической проницаемости он заменил на такой же интеграл с половиной вычета от полюса на вещественной оси (формула Племеля-Сохоцкого). Коэффициент затухания волн с дисперсией, установленной Власовым, ныне носит название «затухания Ландау». Этот факт часто выдаётся  в качестве исправления расчетов Власова. В действительности это не совсем так. Результат Власова относится к случаю, когда в волне отсутствуют захваченные частицы. Если в волне среди захваченных частиц больше тех, скорость которых больше фазовой скорости волны мы будем иметь дело с эффектом Черенкова. Обратный эффект Черенкова, т.е. затухание Ландау будет иметь место, если захвачено больше «медленных» частиц.
     За рубежом работа А.А.Власова получила широкую огласку, по-видимому, после  того, как результаты Власова были воспроизведены Д. Бомом и  И.П.Гроссом  в статье «Теория плазменных осцилляций. А.Происхождение  поведения подобного среде» В Physical Review в 1949 году.
    Среди других важных научных проблем, которые находились в центре внимания А.А.Власова, были проблемы теории каналирования заряженных частиц в кристаллах, проблемы, связанные с разработкой последовательной теории кинетических явлений в твердых телах, включая кинетическую теорию фазовых превращений. В известной монографии М.Борна и Хуан Куня «Динамическая теория кристаллических решёток» (М. 1958) основные выводы о динамике системы делаются на основе механической теории колебаний атомов в окрестностях положений равновесия. Такой подход представлялся А.А.Власову недостаточным. Уравнения колебаний дают возможность получить только функции времени, а для описания волновых процессов в исходных уравнениях в явном виде должны содержаться частные производные по пространственным координатам. «Кристаллическая решетка не выводится в такой теории, а вводится»,- замечал А.А.Власов. Последовательная теория роста кристаллических структур, по Власову, не может быть создана на основе метода, в котором используется классические или квантовые гамильтонианы с модельными потенциалами взаимодействия между атомами. При фазовых превращениях происходит перестройка электронных конфигураций атомов и, следовательно, изменение функциональнай формы потенциалов взаимодействия. Именно изменение со временем формы потенциалов взаимодействия является фундаментальным свойством кинетики  роста кристаллов. А такую временную эволюцию взаимодействий  систем частиц дают уравнения поля. Таким образом, в основу кинетики фазовых переходов должны быть положены уравнения с самосогласованным полем. К сожалению, теория роста кристаллов, основанная на этих принципах, осталась незавершённой. Однако с основами подхода можно ознакомиться в его статье «Нитевидные и пластинчатые структуры в кристаллах и жидкостях» (ТМФ 5,1970).
    25 марта 1982 года было зарегистрировано открытие А.А.Власова, А.А.Введенова, М.А.Яковлева, В.А.Алексеева: «Установлена неизвестная ранее закономерность понижения потенциала ионизации атомов в плотной слабоионизованной плазме (на примере плазмы щелочных металлов), заключающаяся в уменьшении потенциала ионизации с ростом концентрации нейтрального газа в плазме и обусловленная взаимодействием ионов и электронов с нейтральными атомами и притяжением между ионами при посредстве нейтрального газа».
     Представляют интерес и высказывания А.А.Власова по поводу теоретической физики, как профессии. Эту профессию он считал «опасной» с точки зрения потери специализации, потому что между исследователем и  природой возникает экран из математических символов, и велика вероятность принять за действительность её отображение в символах. Для сравнения, приведём предупреждение Ф.М.Морса и Г.Фешбаха в «Методах теоретической физики»: «…но физик-теоретик должен в первую очередь добиваться полного понимания физического смысла употребляемой символики, без чего формальная строгость не может принести ему никакой пользы».
     Сам А.А.Власов был таким настоящим физиком-теоретиком.