Наследие Фурье и проблемы модернизации курса математического анализа для физиков

26 февраля 2019 г. на методологическом семинаре физического факультета был заслушан доклад профессора Д.Д. Соколова «Наследие Фурье и проблемы модернизации курса математического анализа для физиков». Доклад вызвал значительный интерес, среди слушателей было много студентов и аспирантов. Вниманию читателей предлагаются тезисы выступления Соколова.

Полный текст доклада можно прочитать: Д.Д. Соколов, Наследие Фурье и проблемы модернизации курса математического анализа для физиков, Ученые записки Физического факультета Московского университета, N3, 1830101, 1-6, 2018.

Главный редактор «Советского физика»

Знакомство с жизненным путем Жана Батиста Фурье (1768-1830) позволяет много понять в истории Франции, да и в нашей истории — на чужом примере многие общие тенденции становятся виднее. Выходец из социальных низов, Фурье был человеком своего времени. Он активно участвовал — естественно, на стороне революции — в том общественном кризисе, который известен нам как Великая французская революция. Революция подняла его в элиту французского общества. Знаменитые слова Наполеона во время тяжелой битвы в Египте «Ослов и ученых — в середину!» были, в частности, проявлением заботы о Фурье, участвовавшем в походе.

По краткой выжимке из богатой биографии Фурье видно, как работал мощный социальный лифт, обеспечивший поддержку революции. Наука во Франции в формах, сопоставимых с современными, существовала к тому времени уже более столетия, но ученые еще не были властителями дум общества. Однако в поколении Фурье к мнению ученых уже прислушивались лидеры государства. Сам Фурье принимал участие в формировании тех черт французской интеллектуальной элиты, которые во многом определяют жизнь современной Франции, но плохо видны из нашей перспективы. Каждый раз, когда по телевизору говорят о выдающейся роли Сорбонны во Франции, вспоминаешь, что в реальной жизни дело обстоит иначе. Про выпускника Сорбонны говорят — «Он даже не нормальер!», т.е. не выпускник Нормальных школ -- тесно связанных с армией училищ, выпускники которых ценятся гораздо больше выпускников университетов. Мне кажется, что жизненный путь Фурье во многом перекликается и позволяет лучше понять жизненный путь многих великих ученых первого советского поколения, ну, хотя бы, О.Ю. Шмидта.

В разнообразном наследии Фурье глаз лектора уверенно выделяет проблему освоения рядов и интеграла Фурье студентами-физиками, изучающими математический анализ. Эта глава, завершающая курс математического анализа, явно оказывается очень трудной для студентов. Это хорошо видно, например, по посещаемости лекций — лектор теряет в этот момент чуть ли не половину слушателей — их интеллектуальный уровень не позволяет понять смысла принадлежащей Фурье математической конструкции. Пугает перспектива того, что юный физик, покупая новый гаджет, на вопрос продавца о требуемых технических характеристиках устройства, достанет из кармана график, на котором изображена зависимость ожидаемого электрического поля в точке приема от времени. Скорее всего, такого покупателя поместят в психиатрическую лечебницу, откуда он не сможет выйти до конца жизни или, по крайней мере до того момента, когда он узнает, что такое частота, длина волны и другие характеристики радиосигнала, выражающиеся на языке преобразования Фурье.

Сама необходимость модернизации образования вообще и лекционных курсов в частности принадлежит к вечным проблемам человечества. Знатоки говорят, что жалобы на ухудшившееся качество учащихся и их нежелание работать представлены уже в текстах пирамид. Решение этой проблемы не может замыкаться только в рамках научного сообщества. Например, знакомство с гимназическими учебниками конца XIX века приводит к мысли, что отказ от идеи общедоступности образования и переход к усиленному обучению небольшой части молодежи позволил бы, по крайней мере, на какое-то время, резко поднять качество выпускников в любой заданной области науки. Однако подобные простые решения представляются социально неприемлемыми и, видимо, ведут к катастрофическим последствиям. Тем не менее, даже в рамках существующих социальных ограничений можно, видимо, сделать многое для того, чтобы сделать курс математического анализа более доступным для слушателей.

Поясним это на конкретном примере того, как хорошие университетские учебники излагают, скажем, преобразование Фурье. В учебнике Б.М. Будака и С.В. Фомина, который в целом хорошо уловил тенденции развития математической физики, основная идея преобразования Фурье излагается так. При некоторых (не самых простых) условиях для функции f(x) справедливо тождество

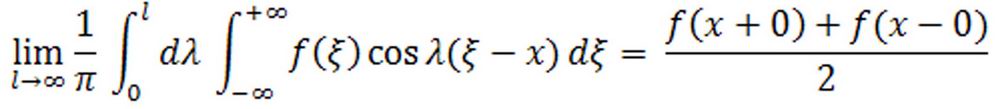
(1)

У думающего студента немедленно возникают два вопроса (у плохого студента, конечно, никаких вопросов не возникает). Во-первых, почему бы не ограничиться для начала только непрерывными f(x) и не писать в правой части тождества (1) просто f(x). Во-вторых, зачем вообще нужно представлять и так известную функцию f(x) через достаточно сложный повторный интеграл, сопровождаемый операцией предельного перехода.

Непосредственно следующее доказательство сформулированной теоремы не облегчает понимание. Смысл его состоит в том, что при l→∞ ядро интегрального преобразования в левой части равенства стремится к δ-функции, что и выражает соотношение (1), однако в тексте понятие δ-функции не возникает.

Конечно, в жизни никто не собирается пользоваться преобразованием Фурье в виде соотношения (1), в огромном большинстве случаев преобразование Фурье записывают в комплексной форме. Оно нужно вовсе не для того, чтобы сложным образом выражать функцию через саму себя. Наконец, соотношение (1) выражает, конечно, мысль о том, что последовательное применение прямого и обратного преобразований Фурье восстанавливает исходную функцию. Это, конечно, полезное свойство, но нельзя сказать, что без него использование идеи Фурье было бы невозможным. Например, суперпозиция прямого и обратного вейвлет-преобразования восстанавливает исходную функцию только с точностью до прибавления константы, но это не особенно препятствует применению этого полезного обобщения преобразования Фурье.

Замечательно, что большинство из этих мыслей в той или иной форме высказаны и разъяснены в тексте учебника (нет только вейвлетов, которые тогда еще не открыли). Другое дело, что для того, чтобы получить ответы на свои вопросы, читатель должен внимательно прочитать весь учебник и сделать не сформулированные явно выводы из его текста. Такой формат текста был труден и для того поколения, которое начинало учиться по этому учебнику, но уж совершенно неприемлем для современных студентов, воспитанных на Википедии и обладающих клиповым сознанием.

Почему же авторы классических учебников выражали свои мысли в такой недружественной для физиков форме и как преодолеть этот разрыв между математической формой и физическим содержанием? Представляется, что дело в том, что математики времен Фурье, времен Вейерштрасса и современности совсем по-разному декларировали предмет своей науки. Для Фурье, а, тем более, для Эйлера не было актуально противопоставление физики и математики. Поэтому непросто сказать, кем был Фурье по преимуществу — физиком, изучавшим проблемы теплопроводности, или математиком, занимавшимся разложением функций в ряды и интегралы, получившие его имя. Видимо, и Эйлера не увлекала задача последовательного изложения содержания математического анализа. Как известно, Эйлер написал первый курс этой науки. Он переведен н а русский язык и при чтении производит сильное впечатление — в книге с трудом опознаются даже разделы, которые в современном курсе связаны с именем Эйлера.

Подобный метод работы привел в начале XIX века к системному кризису в математическом анализе. Выяснилось, что, действуя в духе Эйлера, можно, при желании обосновать самые нелепые и нефизические утверждения. Была осознана необходимость построения математического анализа как последовательной науки. Эта задача была, как известно, выполнена несколькими поколениями математиков (от Коши до Римана и Вейерштрасса и далее), которые явно противопоставили математическое исследование физическому. В наиболее яркой форме этот этап развития математики виден на примере теоремы Римана об условно сходящихся рядах — выбирая подходящий порядок суммирования, можно сделать сумму такого ряда равным любому наперед заданному числу. Между прочим, очень заметная часть рядов и интегралов Фурье, включая ключевые для волновой оптики интегралы Френеля, являются условно сходящимися. К ним в полной мере относится наблюдение Римана. Более того, нет сомнения, что если бы не запросы физики, то в рамках абстрактной математики после работ Римана рассматривались бы лишь абсолютно сходящиеся ряды и интегралы. Этот пример заодно поясняет, почему нельзя систематически рассматривать курс математики для физиков как раздел физики, а необходимо представлять студенту математику как самостоятельную науку. В противном случае начинающему исследователю предстояло бы пережить этот кризис математического анализа на своей собственной шкуре и самостоятельно проделать тот непростой путь, которые за нас проделали математики XIX века.

Переработка математического анализа, предпринятая великими математиками середины и конца XIX века, потребовала своих стандартов математического изложения, концентрации внимания на доказательствах теорем. Потребовалось очень значительное время для того, чтобы довести этот процесс ревизии до уровня университетских учебников. Все это и вылилось в классические университетские учебники, некоторые примеры из которых мы разбирали выше.

Конечно, описанная математическая традиция не была абсолютной — и в XIX, и в XX веках были великие математики, которые могли и хотели работать и как физики. Достаточно назвать работы А. Н. Колмогорова по теории турбулентности, которые с полным правом можно рассматривать как эпохальные работы по физике.

Постепенно стали выявляться слабые места той математической традиции, которая сформировалась в работах классиков математического анализа XIX века. Появились теоремы, которые удачно сочетали строгость и красоту математического исполнения и практическую бесполезность.

Явным признаком того, что в математике есть что-то кроме аксиом, определений, теорем и их доказательств, стало появление компьютеров в середине XX века. Классическая математика отреагировала на это не совсем предусмотрительно — утверждением об очень ограниченной роли компьютеров в собственно математическом исследовании. Как известно, это — не лучший способ ответа на вызовы времени. Однако он продержался примерно 30 лет, до того момента, когда в науку и жизнь широко вошли персональные компьютеры.

В компьютерном мире невозможно читать лекции по математическому анализу, делая вид, что ты не знаешь, чем компьютерная математика отличается от классической математики теорем и доказательств.

По глубокому замечанию великого Гете, между двумя противоположными мнениями лежит не истина, между ними лежит проблема. Именно решением данной проблемы в той или иной форме занимаются сейчас люди, работающие в той области математики, которая близка к физике. Нет особого сомнения, что в историческом будущем эта работа выльется в новый синтез, соединяющий достижения предыдущих этапов. Однако сейчас положение меняется так быстро, что его трудно втиснуть в рамки стандартных учебников. Например, внедрение больших пакетов программ, скажем, пакета Wolfram Mathematica, существенно меняет акценты в этом вопросе. Этот переход можно сравнить с тем, который произошел в экспериментальной физике в момент, когда физик перестал делать свои приборы сам, а стал покупать сложные приборы у специализированных фирм. Вообще, неожиданно оказалось, что некоторые области математики приобрели черты экспериментальной физики, а многие диссертации по математике трудно защищать потому, что в них нет и не нужно никаких теорем.

Как же перестраивать и модернизировать в этой обстановке неопределенности курс математического анализа? По этому вопросу нет единого мнения. Один подход — представленный в первую очередь теми, кто не читает лекций по математическому анализу — предлагает отказаться от преподавания устаревших доктрин и сосредоточиться на чем-нибудь более современном, например, теории групп или дифференциальных форм. Полезность этих математических дисциплин не вызывает сомнения, но при реализации идеи мы сталкиваемся с ограничениями антропологического и социального характера. Проще говоря, в заданное время в студента невозможно впихнуть неограниченно много совершенно новой информации, а отказаться для реализации идеи, скажем, от физического практикума (там тоже не все локализовано на переднем крае науки) представляется, мягко говоря, не совсем взвешенным.

Представляется, что лучше работать в рамках более взвешенного, хотя и менее эффектного подхода. Сохранив выдержавшие испытание временем части курса и уменьшив удельный вес ставших менее значимых разделов (на этом пути удалось, между прочим, на четверть уменьшить число лекционных часов по сравнению с учебными планами времен создания классических учебников), сконцентрировать внимание на практических вопросах и задачах.

Отказаться от представления о том, что курс должен содержать исключительно строго доказанные утверждения, и рисовать перед студентами перспективы развития наук, выросших из классического математического анализа (функционального анализа, топологии, дифференциальной геометрии). В январе сего года Дмитрий Дмитриевич Соколов отметил 70-летний юбилей. Редакция газеты «Советский физик», сокурсники юбиляра от всей души поздравляют Дмитрия Дмитриевича, желают ему крепкого здоровья, новых замечательных достижений в различных областях теоретической и математической физики, астрофизики, фундаментальной и прикладной математики, в которых он продолжает активно работать (спектр его научных интересов поражает!) и успехов в воспитании талантливых учеников.

Профессор Д.Д. Соколов